Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] - Hallo sobat blogger
Pendidikan, Posting yang saya unggah pada kali ini dengan judul Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] , Artikel ini bertujuan untuk memudahkan kalian mencari apa yang kalian inginkan, kami telah mempersiapkan artikel ini dengan baik untuk kalian baca dan ambil informasi didalamnya. mudah-mudahan isi postingan
Artikel Formula Matematika,
Artikel Matematika,
Artikel Teori, yang kami tulis ini dapat kalian pahami dengan baik, semoga artikel ini berguna untuk kalian, jika ada kesalahan penulisan yang dilakukan oleh penulis mohon dimaafkan karena penulis masih newbie. baiklah, selamat membaca.
Judul :
Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] link :
Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ]
Baca juga
- Kumpulan Rumus Matematika SMP Untuk UN, [ diktrus matematika ]
- Contoh Soal dan Pembahasan Persamaan Garis , [ diktrus matematika ]
- KUMPULAN SOAL UJIAN NASIONAL MATEMATIKA SMP/MTS, [ diktrus matematika ]
- Operasi Hitung bilangan bulat MTs/SMP Kelas VII, [ diktrus matematika ]
- Menghitung Luas Selimut dan Luas Tabung, [ diktrus matematika ]
- Soal dan Cara Mengerjakan FPB matematika, [ diktrus matematika ]
- Tips Teknik Jarimatika, [ diktrus matematika ]
- RUMUS DAN CONTOH BANGUN DATAR PART II, [ diktrus matematika ]
- Rumus dan Contoh Matematika Tentang Bangun Datar , [ diktrus matematika ]
- Soal dan Pembahasan UN Matematika SMP/MTS, [ diktrus matematika ]
Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ]
Pada tulisan saya ini saya menggunakan segitiga sembarang agar terlihat berlaku secara umum. Ok, sekarang perhatikan  ABC dibawah ini.
ABC dibawah ini. 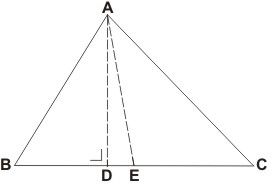
Segitiga ABC diatas memiliki tinggi AD dan Garis Berat AE. Dari gambar diatas diperoleh persamaan
AD2 = AB2 � BD2 � (i)
AD2 = AC2 � CD2 � (ii)
dari (i) dan (ii) diperoleh
AC2 � CD2 = AB2 � BD2
AC2 � CD2 = AB2 � (BC � CD)2 [perhatikan : BD = BC � CD]
AC2 � CD2 = AB2 � (BC2 � 2.BC.CD + CD2)
AC2 � CD2 = AB2 � BC2 + 2.BC.CD � CD2
2.BC.CD = AC2 + BC2 � AB2
CD =  � (iii)
� (iii) atau
AC2 � CD2 = AB2 � BD2
AC2 � (BC � BD)2 = AB2 � BD2 [perhatikan : CD = BC � BD]
AC2 � (BC2 � 2.BC.BD + BD2) = AB2 � BD2
AC2 � BC2 + 2.BC.BD � BD2 = AB2 � BD2
2.BC.BD = AB2 + BC2 � AC2
BD =  � (iv)
� (iv) kemudian substitusi (iv) ke (i), sehingga diperoleh
AD2 = AB2 � BD2
AD =  � (v)
� (v) setelah itu substitusi (iii) ke (ii), sehingga diperoleh
AD2 = AC2 � CD2
AD =  � (vi)
� (vi) Perhatikan  ABC diatas, kita dapat peroleh garis berat AE melalui hubungan garis AD dan CD, yaitu
ABC diatas, kita dapat peroleh garis berat AE melalui hubungan garis AD dan CD, yaitu AE = 
=  [perhatikan : DE = DC - CE]
[perhatikan : DE = DC - CE] =  [perhatikan : CE = BE dan CE =
[perhatikan : CE = BE dan CE =  BC]
BC] = 
=  [karena (ii)]
[karena (ii)] =  [karena (iii)]
[karena (iii)] = 
= 
= 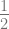

Jadi jika kita memiliki segitiga seperti dibawah ini, maka rumus Garis Berat nya adalah
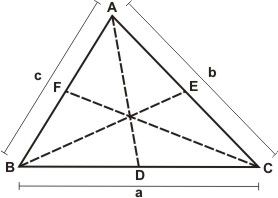
.
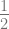
 untuk garis berat AD
untuk garis berat AD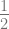
 untuk garis berat BE
untuk garis berat BE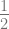
 untuk garis berat CF
untuk garis berat CF.
Apa ada yang bertanya apakah rumus garis berat pada segitiga lainnya seperti segitiga siku-siku, segitiga sama kaki, segitiga sama sisi dan segitiga tumpul sama seperti kasus ini ? Jawabanya, iya sama. Terus pembuktian pada kasus segitiga tumpul bagaimana ? Silahkan dicoba, pembuktiannya sama dengan tulisan ini.
Demikianlah Artikel Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ]
Sekianlah artikel Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] dengan alamat link http://diktrus.blogspot.com/2014/10/rumus-garis-berat-pada-segitiga.html
Related Posts :
- Kumpulan Soal Bangun Datar SMP, [ diktrus matematika ] A. Marilah menyilang (X) huruf a, b, c, dan d pada jawaban yang benar!1. Diketahui alas jajargenjang 20 cm dan tinggi 10 cm, hitung keliling… Read More...
- Kumpulan Soal Peluang SMP kelas 9, [ diktrus matematika ] B. Isilah pertanyan di bawah ini dengan tepat!sebuah dadu berisi 6 dilempar sekali, tentukan peluang :a. muncul angka 3b.&… Read More...
- Contoh Soal dan Pembahasan Bentuk Akar dan Logaritma MTs Kelas 9, [ diktrus matematika ] Bentuk sederhana dari Pembahasan :Jawaban : EDiketahui 3log 6 = p, 3log 2 = q. Nilai 24log 288 = ....Pembahasan :Jawaban… Read More...
- Kumpulan SOAL EKSPONEN DAN LOGARITMA MATEMATIKA SMP/MTs, [ diktrus matematika ] Berikut ini adalah SOAL � SOAL Eksponen dan logaritma yang saya ambil dari SOAL Ujian Nasional tahun 2000 s.d. 2007Materi Pokok : Bentuk aka… Read More...
- Materi SMP PELUANG, [ diktrus matematika ] Beberapa istilah didalam peluang :1. Ruang sampel : Himpunan kejadian yang mungkin dari suatu percobaan2. Titik sampel : semua anggota dari … Read More...
 ABC dibawah ini.
ABC dibawah ini.
 � (iii)
� (iii) � (iv)
� (iv) � (v)
� (v) � (vi)
� (vi) ABC diatas, kita dapat peroleh garis berat AE melalui hubungan garis AD dan CD, yaitu
ABC diatas, kita dapat peroleh garis berat AE melalui hubungan garis AD dan CD, yaitu
 [perhatikan : DE = DC - CE]
[perhatikan : DE = DC - CE] [perhatikan : CE = BE dan CE =
[perhatikan : CE = BE dan CE =  BC]
BC]
 [karena (ii)]
[karena (ii)] [karena (iii)]
[karena (iii)]



0 Response to "Rumus Garis Berat pada Segitiga Matematika, [ diktrus matematika ] "
Posting Komentar