Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] - Hallo sobat blogger
Pendidikan, Posting yang saya unggah pada kali ini dengan judul Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] , Artikel ini bertujuan untuk memudahkan kalian mencari apa yang kalian inginkan, kami telah mempersiapkan artikel ini dengan baik untuk kalian baca dan ambil informasi didalamnya. mudah-mudahan isi postingan
Artikel Formula Matematika,
Artikel Matematika,
Artikel Soal Try Out,
Artikel Teori, yang kami tulis ini dapat kalian pahami dengan baik, semoga artikel ini berguna untuk kalian, jika ada kesalahan penulisan yang dilakukan oleh penulis mohon dimaafkan karena penulis masih newbie. baiklah, selamat membaca.
Judul :
Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] link :
Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ]
Baca juga
- RUMUS DAN CONTOH BANGUN DATAR PART II, [ diktrus matematika ]
- Rumus dan Contoh Matematika Tentang Bangun Datar , [ diktrus matematika ]
- Soal dan Pembahasan UN Matematika SMP/MTS, [ diktrus matematika ]
- Kumpulan Rumus Matematika SMP Untuk UN, [ diktrus matematika ]
- Contoh Soal dan Pembahasan Persamaan Garis , [ diktrus matematika ]
- KUMPULAN SOAL UJIAN NASIONAL MATEMATIKA SMP/MTS, [ diktrus matematika ]
- Operasi Hitung bilangan bulat MTs/SMP Kelas VII, [ diktrus matematika ]
- Menghitung Luas Selimut dan Luas Tabung, [ diktrus matematika ]
- Soal dan Cara Mengerjakan FPB matematika, [ diktrus matematika ]
- Tips Teknik Jarimatika, [ diktrus matematika ]
Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ]
kesebangunan dapat digunakan untuk menghitung tinggi suatu benda yang sulit diukur secara langsung. Suatu pohon yang tinggi menjulang memiliki panjang bayangan 37,5 m di suatu pagi dan 12,5 m di suatu sore. Apabila sinar-sinar garis dari puncak pohon yang menuju tanah membentuk sudut siku-siku, dapatkah kamu menghitung tinggi pohon tersebut?
Sebelum menghitung tinggi pohon tersebut, kita pelajari terlebih dahulu mengenai kesebangunan pada segitiga siku-siku. Perhatikan gambar berikut.
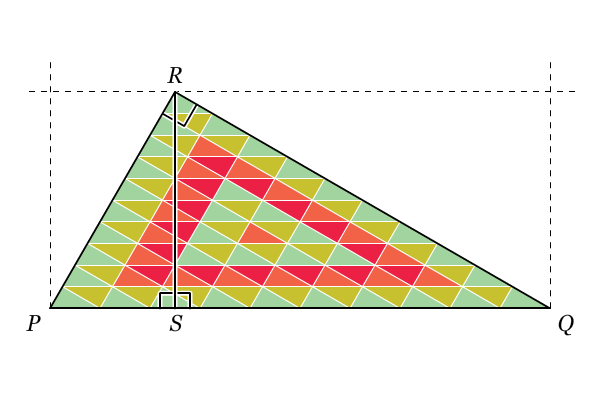
Dari gambar tersebut, apakah kamu menduga bahwa segitiga
PSR sebangun dengan segitiga
RSQ? Dapatkah kamu membuktikannya? Segitiga
PSR memang sebangun dengan segitiga
RSQ. Berikut pembuktiannya.
Perhatikan bahwa sudut
PSR dan sudut
RSQ merupakan sudut siku-siku, sehingga besar sudut
PSR sama dengan sudut
RSQ, yaitu 90�. Selanjutnya, pada segitiga
PRQ, besar sudut
RPS sama dengan 180� dikurangi jumlah dari besar sudut
SQR dan 90�. Demikian juga pada segitiga
RSQ, besar sudut
QRS sama dengan 180� dikurangi jumlah dari sudut
SQR dan 90�.
Sehingga, besar sudut PRQ sama dengan besar sudut QRS. Karena pada segitiga PSR dan segitiga RSQ terdapat dua sudut yang sama besar, maka kedua segitiga tersebut sebangun. Karena segitiga PSR dan segitiga RSQ merupakan segitiga-segitiga yang sebangun, maka perbandingan dari panjang sisi-sisi yang bersesuaian besarnya sama.
Selanjutnya, coba buktikan bahwa segitiga PSR sebangun dengan segitiga PRQ dan segitiga RSQ sebangun dengan segitiga PRQ. Dari kesebangunan segitiga-segitiga tersebut, diperoleh beberapa persamaan berikut.
Sehingga, dari segitiga
PQR dan ruas garis
RS dengan titik
S terletak pada sisi
PQ sedemikian sehingga ruas garis
RS tegak lurus dengan sisi
PQ, diperoleh ketiga persamaan berikut.
RS = v(SP � SQ); RP = v(PS � PQ); dan RQ = v(QS � QP)
Dari persamaan tersebut, kita dapat menghitung tinggi pohon pada permasalahan awal. Tinggi pohon tersebut adalah v(37,5 � 12,5) = 21,65 m
Demikianlah Artikel Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ]
Sekianlah artikel Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] dengan alamat link http://diktrus.blogspot.com/2014/10/kesebangunan-pada-segitiga-siku-siku-ix.html
Related Posts :
- Menghitung Luas Selimut dan Luas Tabung, [ diktrus matematika ] kesempatan kali ini saya sedang piket disekolahan tiba-tiba terfikir untuk posting tentang luas tabung, mungkin postingan kali ini sudah tem… Read More...
- SOAL DAN PEMBAHASAN DERET ARITMATIKA MTS/SMP, [ diktrus matematika ] SOAL 1suatu barisan aritmatika 2, 5, 8, 11. . . dan seterusnya.Tentukanlah :a. suku pertamab. bedac.&nbs… Read More...
- KUMPULAN SOAL UJIAN NASIONAL MATEMATIKA SMP/MTS, [ diktrus matematika ] 1. Suhu mula-mula sebuah lemari pendingin -8�C. Karena listrik padam suhu di dalam lemari pendingin itu naik 2�C seti… Read More...
- Soal dan Pembahasan UN Matematika SMP/MTS, [ diktrus matematika ] Selamat sore sahabat Matematika IT, masih jumpa lagi bersama saya, sambil ngabuburit dan bersantai ria saya teringat kalau tadi pagi untuk s… Read More...
- SOAL DERET ARITMATIKA DAN GEOMETRI, [ diktrus matematika ] Berikut ini adalah soal � soal Barisan dan Deet yang saya ambil dari soal Ujian Nasional tahun 2000 s.d. 2007. Dan bisa dikerjakan menggunak… Read More...

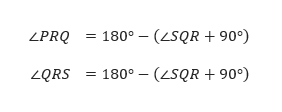


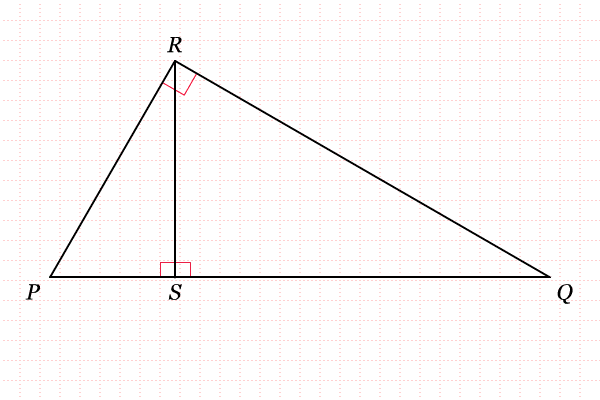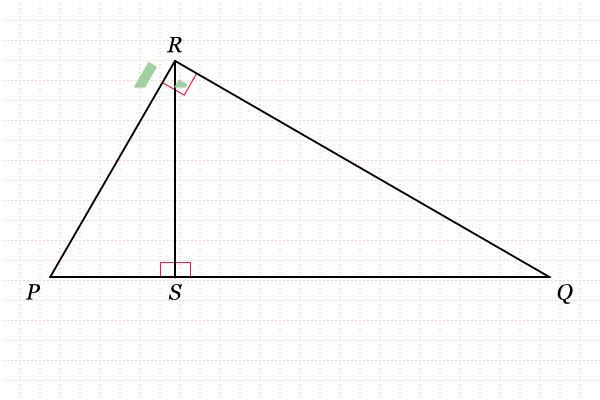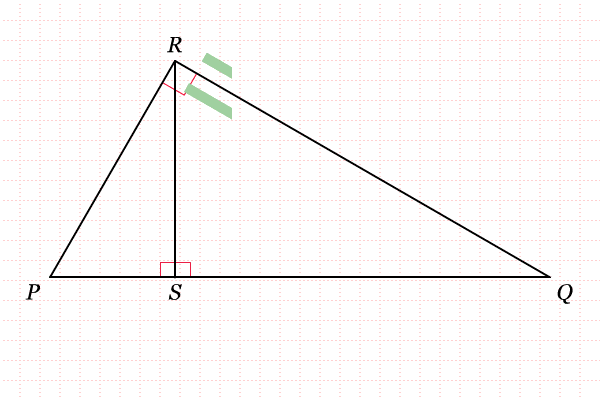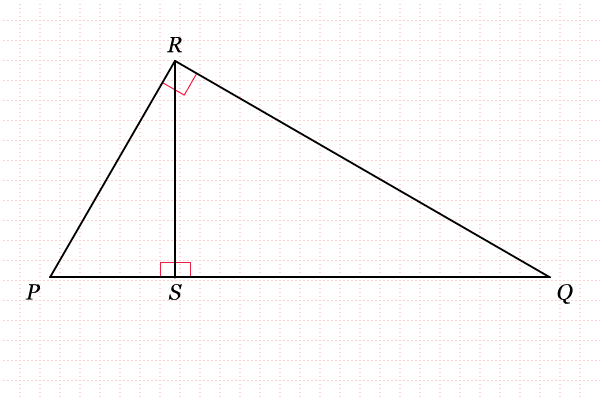
0 Response to "Kesebangunan Pada Segitiga Siku-siku - IX SMP/MTs, [ diktrus matematika ] "
Posting Komentar