Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] - Hallo sobat blogger
Pendidikan, Posting yang saya unggah pada kali ini dengan judul Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] , Artikel ini bertujuan untuk memudahkan kalian mencari apa yang kalian inginkan, kami telah mempersiapkan artikel ini dengan baik untuk kalian baca dan ambil informasi didalamnya. mudah-mudahan isi postingan
Artikel Formula Matematika,
Artikel Matematika,
Artikel Teori, yang kami tulis ini dapat kalian pahami dengan baik, semoga artikel ini berguna untuk kalian, jika ada kesalahan penulisan yang dilakukan oleh penulis mohon dimaafkan karena penulis masih newbie. baiklah, selamat membaca.
Judul :
Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] link :
Pola Bilangan dan Hukum Pascal, [ diktrus matematika ]
Baca juga
- Menghitung Luas Selimut dan Luas Tabung, [ diktrus matematika ]
- Soal dan Cara Mengerjakan FPB matematika, [ diktrus matematika ]
- Tips Teknik Jarimatika, [ diktrus matematika ]
- RUMUS DAN CONTOH BANGUN DATAR PART II, [ diktrus matematika ]
- Rumus dan Contoh Matematika Tentang Bangun Datar , [ diktrus matematika ]
- Soal dan Pembahasan UN Matematika SMP/MTS, [ diktrus matematika ]
- Kumpulan Rumus Matematika SMP Untuk UN, [ diktrus matematika ]
- Contoh Soal dan Pembahasan Persamaan Garis , [ diktrus matematika ]
- KUMPULAN SOAL UJIAN NASIONAL MATEMATIKA SMP/MTS, [ diktrus matematika ]
- Operasi Hitung bilangan bulat MTs/SMP Kelas VII, [ diktrus matematika ]
Pola Bilangan dan Hukum Pascal, [ diktrus matematika ]
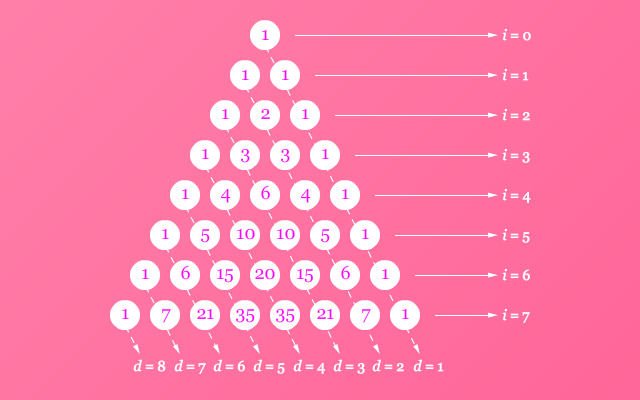
Banyak sekali fakta-fakta menarik dalam segitiga Pascal. Setiap baris pada segitiga Pascal memuat bilangan-bilangan yang merupakan koefisien dari bentuk dari ekspansi pangkat bilangan cacah dari binomial, salah satunya. Akan tetapi, pada pembahasan ini akan dikhususkan untuk menemukan pola bilangan dalam setiap diagonal segitiga Pascal tersebut. Perhatikan gambar berikut.
Untuk menemukan pola tersebut kita akan membutuhkan pola bilangan dalam setiap baris segitiga Pascal. Semua bilangan dalam setiap baris tersebut merupakan koefisien dari ekspansi pangkat dari binomial. Sebagai contoh,
Koefisien dari ekspansi pangkat 4 binomial tersebut adalah 1, 4, 6, 4, dan 1 yang merupakan bilangan-bilangan pada baris ke-4 pada segitiga Pascal. Menurut Teorema Binomial,
Sehingga secara umum barisan bilangan pada baris i = k dalam segitiga Pascal dapat dituliskan,
Sebagai contoh, bilangan ke-2 dan ke-3 dari baris ke-5 segitiga Pascal adalah,
Berdasarkan pola di atas, kita dapat menurunkan rumus untuk menentukan bilangan ai,j, yaitu bilangan yang berada pada baris ke-i dan kolom ke-j dalam segitiga Pascal.
Misalnya, kita dapat menentukan bilangan yang berada pada baris ke-7 dan kolom ke-6 sebagai berikut.
Dari rumus ai,j tersebut, kita dapat menuliskan barisan bilangan pada diagonal ke-d sebagai berikut.
Atau dapat dituliskan sebagai,
Sehingga, suku ke-n dari barisan bilangan pada diagonal ke-d adalah
Sebagai contoh, pada diagonal ke-3 segitiga Pascal merupakan bilangan-bilangan segitiga yang memiliki pola n(n + 1)/2. Barisan ini akan kita uji dengan menggunakan rumus yang baru saja kita temukan. Dengan d = 3,
Demikianlah Artikel Pola Bilangan dan Hukum Pascal, [ diktrus matematika ]
Sekianlah artikel Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] dengan alamat link http://diktrus.blogspot.com/2014/10/pola-bilangan-dan-hukum-pascal-diktrus.html
Related Posts :
- Contoh Soal dan Pembahasan Persamaan Garis , [ diktrus matematika ] Soal 1Tentukan persamaan garis yang melalui titik (2,3) sejajar 2x + 5y - 1 = 0 adalah.......Pembahasan:Cara biasa:Pertama cari gradien… Read More...
- 5 Soal dan Pembahasan Try Out Matematika SMP, [ diktrus matematika ] Soal 1:Keliling segitiga siku-siku adalah 56 cm. Jika panjang sisinya berturut-turut x cm, (3x + 3) cm, dan (4x � 3) cm, maka luas segitiga … Read More...
- SOAL DAN PEMBAHASAN DERET, [ diktrus matematika ] Diketahui sebuah deret 27, 64, 18, 48, 12, 36, ..... tentkan baris deret selanjutnyaa. 8, 27b. &nbs… Read More...
- Soal dan Pembahasan Matematika SMP, [ diktrus matematika ] * SoalHasil dari 6 � 18 : (-2) � 3 adalah ....A. 9 … Read More...
- Soal dan Pembahasan UN Matematika - 1, [ diktrus matematika ] Soal 1:Keliling segitiga siku-siku adalah 56 cm. Jika panjang sisinya berturut-turut x cm, (3x + 3) cm, dan (4x � 3) cm, maka luas segitiga … Read More...
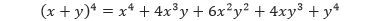
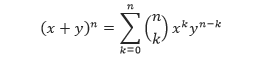
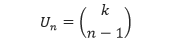
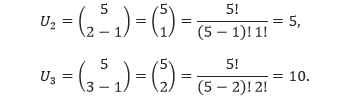
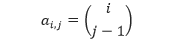
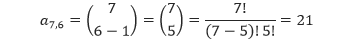
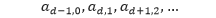
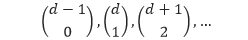
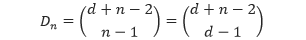
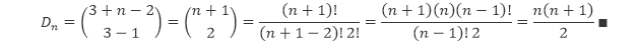
0 Response to "Pola Bilangan dan Hukum Pascal, [ diktrus matematika ] "
Posting Komentar