Judul : Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ]
link : Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ]
Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ]
Pada bagian ini akan dibahas mengenai metode alternatif dalam menentukan volume benda putar. Metode ini disebut metode kulit tabung (shell method) karena metode ini menggunakan volume dari kulit tabung. Perhatikan persegi panjang di bawah ini dengan t adalah panjang dari persegi panjang, l adalah lebar persegi panjang, dan p adalah jarak antara sumbu putaran dengan pusat dari persegi panjang.
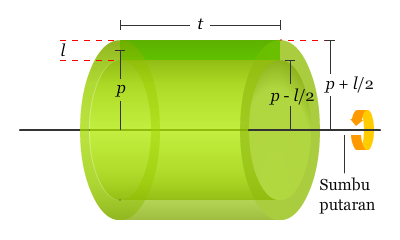
Ketika persegi panjang tersebut diputar menurut sumbu putarannya maka akan dihasilkan kulit tabung dengan ketebalan l. Untuk menentukan volume kulit tabung tersebut, perhatikan dua tabung (tabung luar dan dalam) yang nampak pada gambar di atas. Jari-jari tabung yang lebih besar merupakan jari-jari luar dari kulit tabung, dan jari-jari dari tabung yang lebih kecil merupakan jari-jari dalam dari kulit tabung. Karena p adalah rata-rata dari jari-jari kulit tabung, dan diketahui bahwa jari-jari luarnya p + l/2 dan jari-jari dalamnya p � l/2.
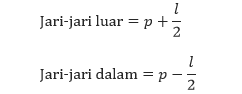
Maka, volume dari kulit tabung adalah

Rumus di atas dapat digunakan untuk menentukan volume dari benda putar. Anggap bidang datar pada gambar di bawah diputar menurut sumbu putarnya sehingga dihasilkan suatu benda putar.
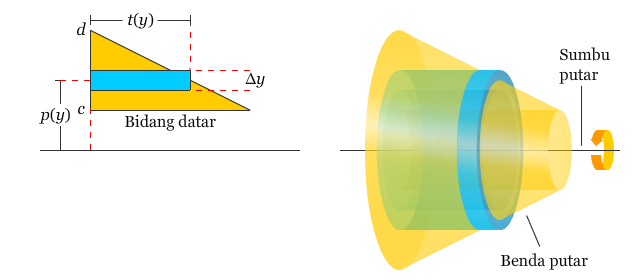
Apabila diperhatikan lebar dari persegi panjang tersebut adalah ?y, maka persegi panjang yang diputar terhadap garis yang sejajar dengan sumbu-x akan menghasilkan suatu kulit tabung yang volumenya
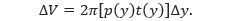
Volume dari benda putar di atas dapat didekati dengan menggunakan volume n kulit tabung yang tebalnya ?y, tinggi t(yi) dan rata-rata jari-jarinya p(yi).
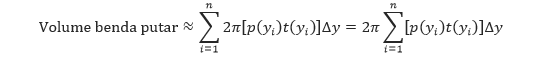
Pendekatan ini akan semakin baik dan semakin baik jika ||?|| ? 0 atau n ? 8. Sehingga, volume benda putar tersebut adalah
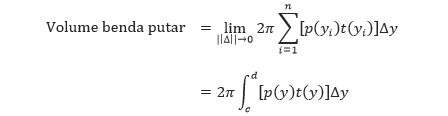
Jadi, dari perhitungan di atas telah ditemukan rumus alternatif yang dapat digunakan untuk menentukan volume benda putar. Perhatikan kesimpulan berikut.
METODE KULIT TABUNG
Untuk menentukan volume benda putar dengan metode kulit tabung, gunakan salah satu dari rumus berikut, seperti yang ditunjukkan oleh gambar di bawahnya.
Sumbu putarnya horizontal,
Sumbu putarnya vertikal,
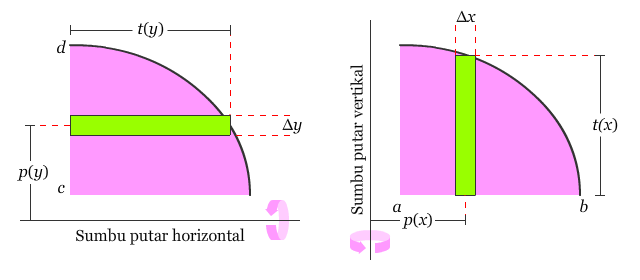
Untuk lebih memahami dalam menentukan volume benda putar dengan menggunakan metode kulit tabung, perhatikan beberapa contoh berikut.
Contoh I: Penggunaan Metode Kulit Tabung untuk Menentukan Volume
Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh
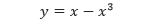
dan sumbu-x (0 = x = 1) dengan sumbu putarannya adalah sumbu-y.
Pembahasan Karena sumbu putarannya vertikal, gunakan persegi panjang vertikal, seperti yang ditunjukkan oleh gambar di bawah.
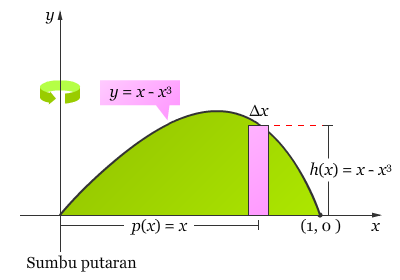
Ketebalan ?x mengindikasikan bahwa x merupakan variabel dalam proses integrasi yang akan dilakukan. Jarak antara pusat persegi panjang dengan sumbu putaran adalah p(x) = x, dan tingginya adalah
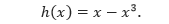
Karena rangenya antara 0 sampai 1, maka volume benda putar yang terbentuk dapat ditentukan sebagai berikut.
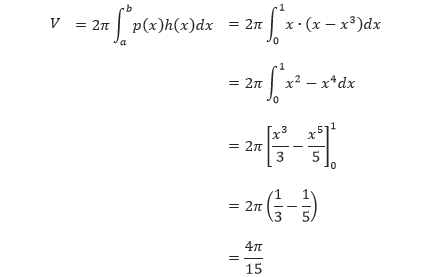
Contoh II: Penggunaan Metode Kulit Tabung untuk Menentukan Volume
Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh
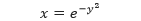
dan sumbu-y (0 = y = 1) dengan sumbu-x sebagai sumbu putarnya.
Pembahasan Karena sumbu putarannya horizontal, gunakanlah persegi panjang horizontal, seperti yang ditunjukkan gambar di bawah ini.
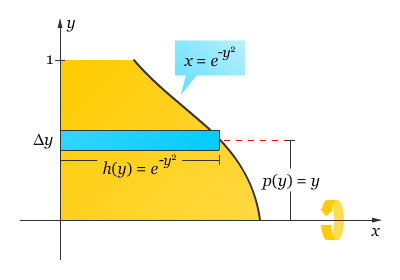
Jarak antara pusat persegi panjang dan sumbu putarannya adalah p(y) = y, dan panjang dari persegi panjangnya adalah
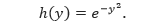
Karena range dari y dari 0 sampai 1, maka volume benda putarnya dapat ditentukan sebagai berikut.
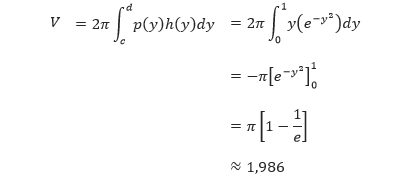
Demikianlah Artikel Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ]
Sekianlah artikel Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ] dengan alamat link http://diktrus.blogspot.com/2014/10/aplikasi-kalkulus-volume-tabung-diktrus.html
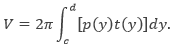
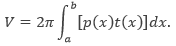
0 Response to "Aplikasi Kalkulus Volume Tabung, [ diktrus matematika ] "
Posting Komentar