Judul : Formula Turunan Lengkap, [ diktrus matematika ]
link : Formula Turunan Lengkap, [ diktrus matematika ]
Formula Turunan Lengkap, [ diktrus matematika ]
Definisi Turunan Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :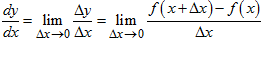 
2.Rumus- Rumus Turunan Dengan menggunakan definisi turunan dapat diturunkan sejumlah rumus tentang turunan, yaitu:
* Jika
dengan C dan n konstanta real, maka : 
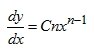
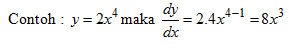
* Jika y = C dengan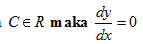
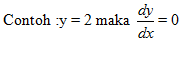
* Jika y = f(x) + g(x) maka
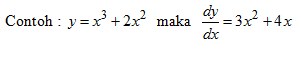
* Jika y = f(x).g(x) maka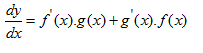
*
*
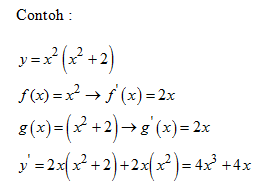
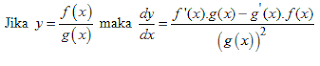
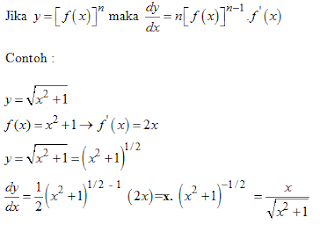
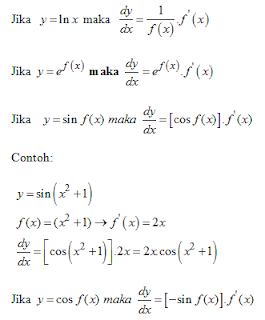
3. Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan
. Turunan kedua diperoleh dengan menurunkan turunan pertama.
Contoh :
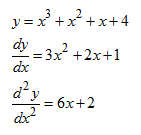
4. Penggunaan Turunan* Menentukan gradien garis singgung kurva
Misal garis g menyinggung kurva y = f (x) dititik (a,f(a)) maka gradien g adalah :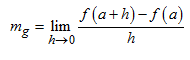
Contoh :
Tentukan gradien garis singgung kurva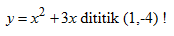
Jawab :
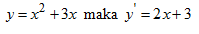
Gradien garis singgung kurva dititik (1,4) adalah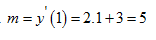
* Menentukan interval naik dan turun
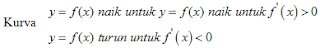
Interval yang memenuhi dan
dan ditentukan denggan menggambarkan garis bilangan dari f '(x) .
Contoh :
Tentukan interval fungsi naik dan turun dari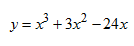
Jawab :
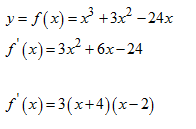
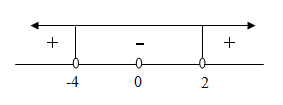
* Menentukan nilai maksimum dan minimum
Nilai maksimum dan minimum fungsi sering disebut nilai ekstrim atau nilai stasioner fungsi tersebut. Nilai ekstrim dari fungsi y = f(x) diperoleh pada f '(x) = 0
Contoh :
Jika
maka nilai stasionernya adalah :
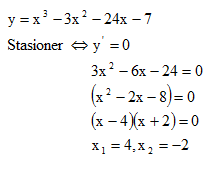
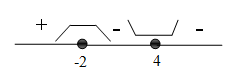
*Fungsi maksimum pada x=-2, maka nilai balik maksimumnya :
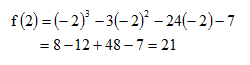
* Fungsi minimum pada x=4, maka nilai balik minimumnya :
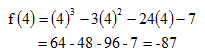
3. TURUNAN FUNGSI TRIGONOMETRI
Rumus-rumus Turunan fungsi Trigonometri adalah:
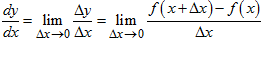
2.Rumus- Rumus Turunan Dengan menggunakan definisi turunan dapat diturunkan sejumlah rumus tentang turunan, yaitu:
* Jika
dengan C dan n konstanta real, maka : 
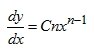
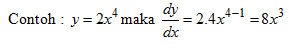
* Jika y = C dengan
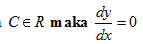
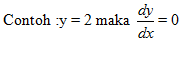
* Jika y = f(x) + g(x) maka
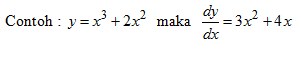
* Jika y = f(x).g(x) maka
*
*
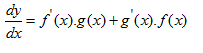
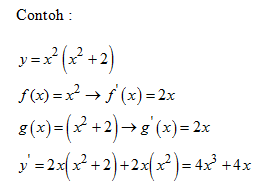
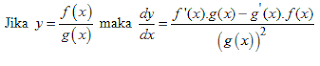
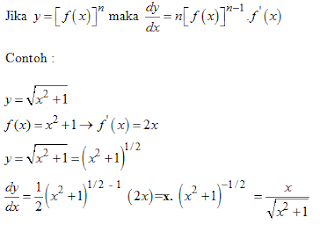
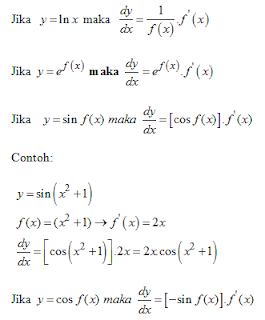
3. Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan
. Turunan kedua diperoleh dengan menurunkan turunan pertama. Contoh :
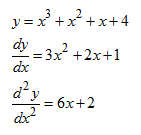
4. Penggunaan Turunan* Menentukan gradien garis singgung kurva
Misal garis g menyinggung kurva y = f (x) dititik (a,f(a)) maka gradien g adalah :
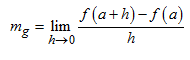
Contoh :
Tentukan gradien garis singgung kurva
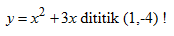
Jawab :
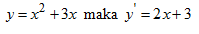
Gradien garis singgung kurva dititik (1,4) adalah
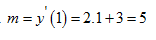
* Menentukan interval naik dan turun
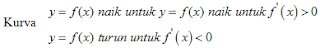
Interval yang memenuhi dan
dan ditentukan denggan menggambarkan garis bilangan dari f '(x) . Contoh :
Tentukan interval fungsi naik dan turun dari
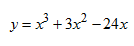
Jawab :
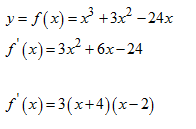
* Menentukan nilai maksimum dan minimum
Nilai maksimum dan minimum fungsi sering disebut nilai ekstrim atau nilai stasioner fungsi tersebut. Nilai ekstrim dari fungsi y = f(x) diperoleh pada f '(x) = 0
Contoh :
Jika
maka nilai stasionernya adalah :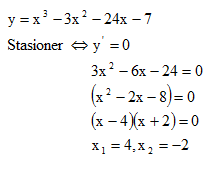 
*Fungsi maksimum pada x=-2, maka nilai balik maksimumnya :
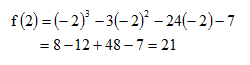
* Fungsi minimum pada x=4, maka nilai balik minimumnya :
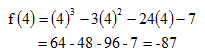
3. TURUNAN FUNGSI TRIGONOMETRI
Rumus-rumus Turunan fungsi Trigonometri adalah:
Contoh Soal:
1.
Jawab:
2.
.......... Jawab:
Demikianlah Artikel Formula Turunan Lengkap, [ diktrus matematika ]
Sekianlah artikel Formula Turunan Lengkap, [ diktrus matematika ] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Formula Turunan Lengkap, [ diktrus matematika ] dengan alamat link http://diktrus.blogspot.com/2014/10/formula-turunan-lengkap-diktrus.html
0 Response to "Formula Turunan Lengkap, [ diktrus matematika ] "
Posting Komentar